- Details
-
Published: Wednesday, 22 March 2023 04:33
-
Hits: 1343
Periodic Table, Atoms and Elements:
Periodic Table is one of the cornerstone of Chemistry. Before we learn periodic table, we should know a bit about atoms and how were they born.
It's believed that a "big bang" took place 14 Gya, and everything came into existence following that. Read more about "Birth of Universe" in Astronomical section.
Over there, we learned about the very first sub atomic particles, and the formation of Hydrogen and Helium atoms. Here we'll see all the atoms and the elements they form.
Atoms & Elements:
All matter that we see is atoms. There are atoms of gold, nickel, oxygen, etc. So, we have silver in pure form which consists of silver atoms. We can't divide an atom further down. Each atom has a nucleus in the center which is composed of protons and neutrons, and a cloud around it which is composed of electrons. As we saw above, neutrons and protons are formed from 3 quark particles, and an electron is a lepton. These come together to form an atom, with nucleus in the center and electron revolving around it (just like planets revolve around the sun)
Atoms of different elements have different number of electrons, protons and neutron. The characteristic thing that defines an element is the number of protons. We can't change the number of protons for a given element. If we somehow change it, than that element gets converted into another element which has that many protons. So, number of protons is called as Atomic number (Z) of an element. No 2 elements have same atomic number.
Mass, Charge and size of e, p, n:
| Particle |
mass |
charge |
size |
| Proton (p) |
1.67x10^-27 kg = 1.007 amu (atomic mass unit) |
+1.6x10^-19C (+ve charge) |
1.7x10^-15m = 1.7fm (femto meter) |
| Neutron (n) |
same mass as proton = 1.008 amu |
No charge (neutral) |
same size as proton = 1.7fm |
| Electron (e) |
9.11x10^-31 kg = 1/1800 amu |
-1.6x10^-19C (-ve charge) |
point particle (no size) |
Unified amu: amu is also written as unified amu or "u". So, you will see mass of proton written as 1u too (instead of 1amu). Mass of a proton is actually 1.007u and mass of neutron is 1.008u (so, both are slightly heavier than 1u). 1u = 1.6605x10^-27 kg
All of these electron, proton, neutron would seem like particle, but modern quantum theory states that quantum scale objects have wave-particle duality, and exhibit both wave like and particle like properties. There have been many controversies over this wave-particle nature of objects, but is now generally accepted. Bigger the size of object, it's wave characteristics become so small, that it acts like a particle fr most practical purpose. However, for very small objects, as electrons, wave characteristics are noticeable. Similarly all electromagentic radiation (i.e light, heat), etc are assumed to hold both wave and particle characteristics to help explain many phenomenon which can't be explained by assuming only a particle mode, or only a wave model.
For our purpose, we will treat all electron, proton and neutron as particles, with the understanding that they show wave properties. All of them have mass, but their mass is too small (neutron/proton have 1800 times greater mass than electron, but still small). So, gravitational forces between these masses is too small. They are held together via electrostatic forces (forces b/w opposite charges).
Electron is considered point particle with no size. Size of an atom is around 10^-10m, which is about 100,000 times larger than size of proton and neutron. So, the nuclues of an atom is very small of the order of fm, with 99.99% of the space around it formed by the electron cloud. Two atoms aren't able to get very close to each other because the repulsive force of this electron cloud prevents the nuclei from getting too close. Size of an atom is determined entirely by it's electron cloud.
A neutral atom of an element has same number of protons and electrons, as the atom is electrically neutral. It's mass number (A) is equal to the sum of number of protons and neutrons (since protons and neurons have mass of 1 amu, the atomic weight of atoms is almost same as atomic number, but not always. The man reason for this is presence of isotopes which will be explained later).
Mass number of Atom (A) = p + n
Atomic number of atom (Z) = p
Given Mass Number and Atomic number of atom, we can figure out the number of electrons, protons and neutrons.
Ex: Na has Z=11, A=23 => p=11, e=11, n=23-11=12.
Isotopes: These are elements which have same proton, but different number of neutrons. Look in "Nuclear Chem" section.
Periodic Table:
We saw above how the number of protons is what defines an element. This wasn't known to mankind, and a lot of thinkers were trying to come up with some theory on what makes an element unique. The first periodic table to become generally accepted was that of the Russian chemist Dmitri Mendeleev in 1869: This wikipedia link has details of all elements in Periodic Table: https://en.wikipedia.org/wiki/Periodic_table
This is a pictorial periodic table: https://periodictable.com/
This is another periodic table that shows certain properties of all atoms in periodic table: https://www.periodic-table.org/
The very first thing to know in a periodic table is that Elements are organized by number of protons they have, which start from 1 proton for Hydrogen, all the way to 110+ protons for some heavier elements. This is known as "Atomic Number". However what determines the properties of any element is NOT the number of protons, but the number of electrons. However, it's not just the raw number of electrons, but electrons in the outer shell (and also the subshell they are in) that mostly determine most of the electrical and chemical behavior of the element. Since elements are neutral in charge, number of electrons is bound to be the same as the number of protons. We can make these atoms lose or gain electrons or share electrons via chemical reactions, in which case they may become charged.
Today, 118 elements are known, the first 94 of which are known to occur naturally on Earth at present.
Periodic Table trend (this will be more relevant once you cover the contents in this section) => https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_and_Websites_(Inorganic_Chemistry)/Descriptive_Chemistry/Periodic_Trends_of_Elemental_Properties/Periodic_Trends
Electron Orbit:
Atoms have energy shells, which are the shells or space around the nucleus where electrons are to be found. The reason electrons can only be found in these distinct spaces around the nucleus is because electrons can only have certain distinct energies. These distinct spaces are called electron orbital. Pauli's Exclusion principle states that no 2 electrons can have the same energy state, implying each orbital (which is a energy state) can have a max of 2 electrons, one with +ve spin and one with -ve spin. If we had only single spin for electrons, then there could have been only 1 electron per orbital.
Bunch of electron orbitals are grouped into sub shells which are further bundled into shells. There are 4 sub shells named as s,p,d and f. s has only 1 orbital, so can have max of 2 electrons, p has 3 orbitals and so a max of 6 electrons, d has 5 orbitals, and so a max of 10 electrons, and f has 7 orbitals and so a max of 14 electrons. "s" is spherical orbital, "p" is dumb bell shaped, d and f are more complex. These shapes represent the three-dimensional regions within which the electron is likely to be found with a 90% probability. When Scientists in early 1900 started studying atoms, they became aware of the shells (Bohr's model), but didn't know about the existence of sub shells. They knew by looking at spectral lines emitted by these atoms that some spectral lines were more intense than others, but didn't know the reason. Reason turned out to be these sub-shells that were present within a single shell. The designations s, p, d, and f result from those early historical attempts to classify atomic spectral lines. (The letters stand for sharp, principal, diffuse, and fundamental, respectively.) After f, the letters continue alphabetically as g, h, i, j, etc. So, sub-shells can be thought of as finer granularity of a shell => When you look at a shell closely, you see it's not one but rather is composed of bunch of sub shells.
The shells are numbered from shell=1 to shell=7. Each shell can have max of 2*n^2 electrons. So shell1 can have max 2 electrons, shell2=8 electrons, shell3=18 electrons, shell4=32 electrons. shell5=50 electrons and so on. It's not the total number of electrons in an atom, but rather the number of electrons in outer shells (rather outer sub shell) that determines the properties of elements. Hence all elements with same number of electrons in outer sub shell are put into same column, to indicate that they have similar properties. Rows are automatically formed due to this, as the elements are put in increasing order of their Atomic number. So, if an element has 3 electrons in n=2, then elements with 3 electrons in n=3, n=4, n=5 etc will all have similar properties.
Shells are numbered as follows:
- 1n => 1st shell has only 1 sub shell = 1s (max 2 electrons)
- 2n => 2nd shell has 2 sub shells s,p = 2s (max 2 electrons) and 2p (3 of these have max 6 electrons)
- 3n => 3rd shell has 3 sub shells s,p,d = 3s (max 2 electrons), 3p (max 6 electrons) and 3d (5 of these have max 10 electrons)
- 4n => 4th shell has 4 sub shells s,p,d,f = 4s (max 2 electrons), 4p (max 6 electrons), 4d (max 10 electrons) and 3f (7 of these have max 14 electrons)
- 5n to 7n => 5th to 7th shells are filled in slightly intricate ways which are shown in diagram below.
Electrons are filled in orbitals starting from lowest energy orbital to highest energy orbital. It turns out that our numbering system above is not in same order as increasing energy level, i.e we would expect 3d to be lower in energy than 4s based on numbering, but in reality, 4s is lower in energy than 3d. The simple reason is that orbitals for n=3 and higher tend to get closer to each other, and so the energy levels are very close. This results in some subshells from lower "n" having higher energy than subshells in higher "n". Below is the correct order of increasing energy:
1s ≪ 2s < 2p ≪ 3s < 3p ≪ 4s < 3d < 4p ≪ 5s < 4d < 5p ≪ 6s < 4f < 5d < 6p ≪ 7s < 5f < 6d < 7p ≪ ... (Here the sign ≪ means "much less than" as opposed to < meaning just "less than"). The way to remember this sequence is very easy, and is in the wiki link above for periodic tables. It's called the "Aufbau Principle/rule".
NOTE: The above energy rule s not true for all elements. It works for elements until 4s2 (Calcium), but then for transition elements, things change. Since we said above that 3d has higher energy than 4s
Orbital filling => https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Electronic_Structure_of_Atoms_and_Molecules/Electronic_Configurations/The_Order_of_Filling_3d_and_4s_Orbitals
Behaviour of electron's is described by 4 quantum numbers (QN):
- Principal QN (n) => This is the shell number n shown above. This is the main shell that determines the distance from nucleus.
- Angular Momentum QN (l) => This ranges from 0 to n-1, and relates to shape of orbital (i.e denotes sub shells s, p, d, f, etc). So for n=2, we will have 2 values of l=0, 1. l=0 => s orbital while l=1 => p orbital, and so on.
- Magnetic QN (m) => this ranges from -l to +l. So for l=1, it has 3 values -1, 0, +1. This determines the orientation of sub shell. Sp, p subshell above can have 3 orientations as m can have 3 values. These 3 orientations are in x, y and z direction.
- Spin QN (s) => This is the orientation of electron spin, and can have only 2 values => +1/2 and -1/2.
Pauli's exclusion principle => No 2 electrons can have the same QN. i.e all n. l, m and s can't be same for 2 electrons within an atom.
The electron cloud diagram shows the region where an electron has 90% probability of being found. S is spherical, p is dumb bell shaped, d and f are more complex shapes.The shapes grow bigger with inc "n" as sub shells are further away from nucleus. The shapes are very important, as that is where the bonding takes place with other atoms. So, the net shape of the compound is dictated by orbitals participating in bonding.
This video has further description => https://www.youtube.com/watch?v=Ewf7RlVNBSA
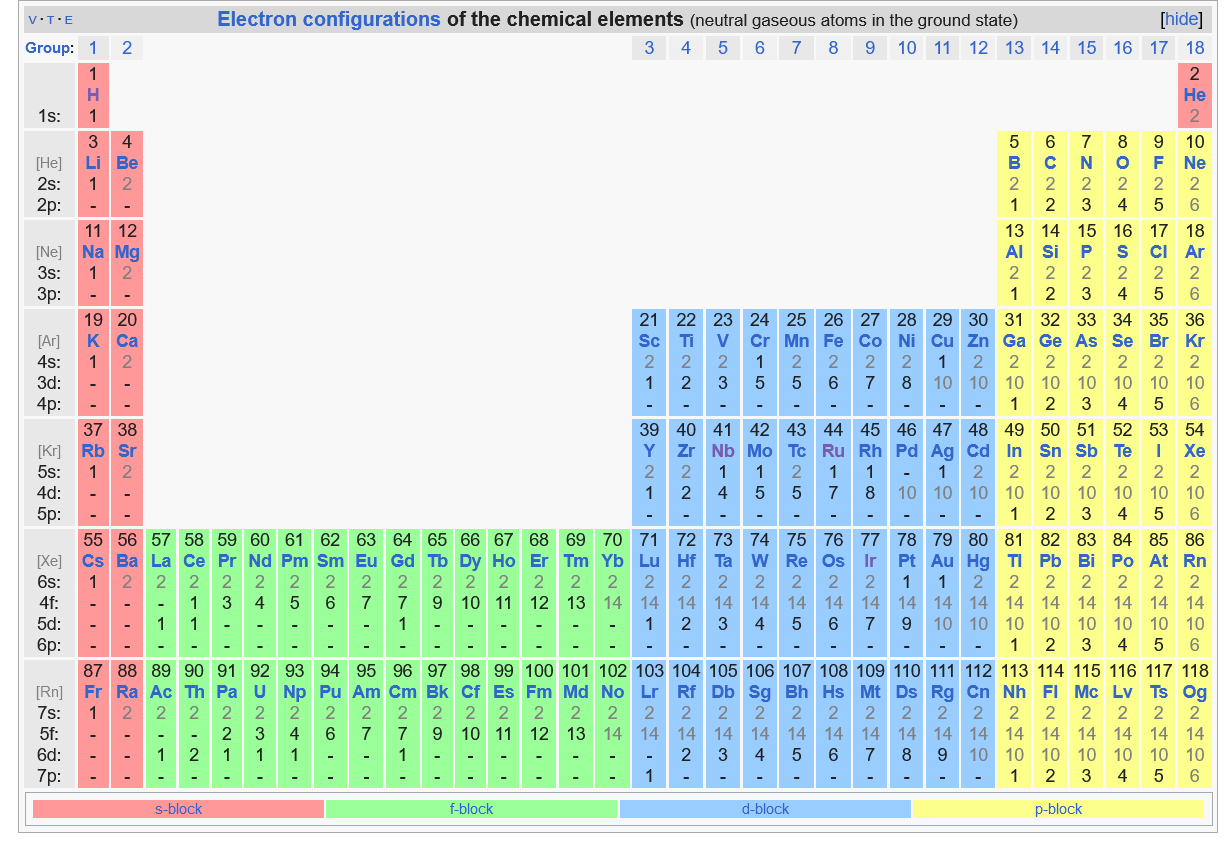
Below is the Periodic Table showing electron distribution in various shells and sub sells. As can be seen, the order of increasing energy is followed. So, electrons start filling up in above order starting from Hydrogen (first element in periodic table) with only 1 electron, all the way to Oganesson (last element in periodic table) with 118 electrons. There are some elements for which the electrons are filled in higher level sub-shell, before lower level sub-shell are filled (ex: copper, silver, gold, etc have only 1 electron in their "s" sub shell, even though they should have 2. Instead that 1 electron moves to higher "d" subshell). This exception happens because 2 half filled sub shells are more stable than "1 full sub shell and one close to half subshell". This is called "exception to Aufbau Principle" and is particularly seen in higher "n", where diff in energy b/w sub shells is smaller, and hence increasing tendency for this to happen.
Elements are organized in rows and columns. There are 7 rows for 7 shells (n=1 to n=7). Elements in a row don't share any properties in common. There are 18 columns (total number of columns is 32, but they are usually numbered from 1 to 18. The higher columns from 19 to 32 are are not important as they are "f block" elements and hence not numbered). The 1st column has 1 electron in outermost shell, 2nd column has 2 electrons in outermost shell and so on, until we reach the 32nd column which should have 32 electrons in the outer most shell. But because of the abnormal reordering of energy levels of sub shells, we get to a higher level shell before we are able to completely fill a lower level shell.
- 1st row: For n=1, max # of electrons is 2, so only 2 entries in 1st row. subshell=1s
- 2nd row:For n=2, max # of electrons is 8, so only 8 entries in 2nd row. sub shells=2s, 2p
- 3rd row:For n=3, max # of electrons is 18, so there should be 18 elements, but only 3s and 3p fill up. Before 3d fills up, 4s starts filling up, so only 8 elements are here with sub shells = 3s, 3p
- 4th row: For n=4, max # of electrons is 32, so there should be 32 elements, but we have 3d left over from n=3. So, we fill 4s, 4p and 3d.
- 5th row: For n=5, max # of electrons is 50, so there should be 50 elements, but we have 4d and 4f left over from n=4. So, we fill 5s, 4d and 5p.
- 6th row: For n=6, max # of electrons is 72, so there should be 72 elements, but we don't ever get there as there are already so many sub shells left unfilled from n=4 and n=5. We fill in order of 6s, 4f, 5d and 6p
- 7th row: For n=7, max # of electrons is 98, so there should be 98 elements, but we don't ever get there as there are already so many sub shells left unfilled from n=5 and n=6. We fill in order of 7s, 5f, 6d and 7p
Atom Formation:
As we saw above, atoms were formed from protons, neutrons and electrons coming together.
Hybrid Orbitals:
A very simplistic explanation was shown above where s has single orbital with spherical shape, p has 3 orbitals in 3 dimension of x,y,z, while d has 5 orbitals along 5 orientations, etc. For some elements in periodic table, it was observed that when these atoms came close to each other, the shape of the lattice structure formed didn't match our above theoretical expectation. These newer shapes prompted concept of hybrid orbitals => Some of these s and p orbitals mix up to form hybrid orbitals which are a mix of s and p orbitals. This happens only for 5 elements in 2nd row => Be, B, C, N and O. Of these, C, N and O comprise most of the compounds found in nature, so we'll look at these 3:
C => 2s2 and 2p2 hybridize to 4 2sp3 hybrid orbitals. It forms a tetrahedral shape. Tetrahedral shape allows the 4 vertices in a 3D shape to be equidistant from each other. It's called sp3 orbitals to indicate that it has 25% s character and 75% p character
Proof of tetrahedron 1090 angle here: https://www.ctralie.com/Teaching/Tetrahedron/
hybrid orbitals => https://www.youtube.com/watch?v=vHXViZTxLXo
- sp3 hybrid orbitals => For Carbon, 4 sp3 hybridized orbitals with 1 electron in each. The bonds formed are called sigma bonds,
- sigma bond => single bond with only 1 electron being shared. In CH4, there are 4 single C-H bonds, each of which is sigma bond (4 sp3 hybrid orbitals formed)
- sp2 hybrid orbitals => For Carbon, 3 sp2 hybridized orbitals with 1 electron in each. One remaining 2p orbital doesn't hybridize and retains it's 2p identity. 1 bond formed b/w 2 C atom is sigma bond, but 1 bond in the double bond is a pi bond.
- Pi bond => double bond with 2 electrons being shared results in 1 bond being sigma bond and other one being pi bond. In C2H4 , there is 1 double bond b/w C=C (which is 1 sigma bond and 1 pi bond), and then 4 single C-H bonds, each of which is sigma bond (2 sp3 hybrid orbitals formed)
- sp1 hybrid orbitals => For Carbon, 2 sp hybridized orbitals with 1 electron in each. Two remaining 2p orbital don't hybridize and retain their 2p identity. 1 bond formed b/w 2 C atom is sigma bond, but 2 bonds in the triple bond are pi bonds.
- Pi bond => triple bond with 3 electrons being shared results in 1 bond being sigma bond and other two being pi bond. In C2H2 , there is 1 triple bond b/w C≡C (which is 1 sigma bond and 2 pi bonds), and then 4 single C-H bonds, each of which is sigma bond (2 sp1 hybrid orbitals formed)
Water's tetrahedral shape => Above vid explains why water has 109 degree angle b/w the 2 H atoms. It's because of hybridization.
Bohr's Model:
A very simplistic explanation of various observed properties of Hydrogen like atoms was proposed by Neil Bohr's model in 1913, which matched exactly with what was observed in Experiments. Bohr's model is not correct, nor does it explain behaviour of other atoms, but it was a big step in understanding atoms. It was based on Classical Physics (or Newtonion Physics). In 1926, Schrodinger explained properties of all atoms based on his famous Schrodinger Equation which was a departure from Classical Physics into Quantum Physics. Schrodinger Equation is the one that is the accepted one, however it's very complex and not solvable for larger atoms.
Here's the derivation of Eqn based on Bohr's model: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Chemistry_(Blinder)/01%3A_Chapters/1.07%3A_Hydrogen_Atom
Force b/w proton and electron of hydrogen atom = q1*q2/(4*pi*ε0*r^2) = -e^2/(4*pi*ε0*r^2)
Potential Energy of system at distance r is d(E) = - ∫F.dr => E = - ∞R∫F.dr = - (-(-e^2/4*pi*ε0*r))]∞R = --e^2/(4*pi*ε0*R) (potential energy is -ve meaning it takes energy to separate them. The energy at infinity is 0, so -ve energy means energy is going lower, i.e sytem is losing energy. So, +ve energy has to be supplied or work has to be done to bring it back to 0 energy).
Since electron is moving in a circle, a centripetal force is needed as per Newton's law, i.e m*v^2/R = F => m*v^2/R = e^2/(4*pi*ε0*R^2) => Eqn (1)
Total energy of the Atom = T(Kinetic Energy of electron) + V(Potential Energy of electron-proton) = 1/2*(e^2/4*pi*ε0*R) - e^2/4*pi*ε0*R = -1/2*(e^2/(4*pi*ε0*R)) => (Total energy is -ve, meaning energy was lost in bringing the electron-proton system together. So, energy has to be supplied if we want to break this sytem and take charges to infinity. Energy needed will be +1/2*(e^2/(4*pi*ε0*R). So, where did this energy get lost? Well, there must have been electromagnetic waves that were emitted out when nucleus with proton and electron came close by to form a system of electron orbiting around the proton. This resulted in some energy lost out. This is exactly the energy that has to be provided to this system to break apart this electron-proton system. Usually it's provided by absorbing some light wave.)
Total Energy of atom is -ve => Energy has to be supplied to bring it to 0, i.e break it apart.
There are 2 variables, speed v and Radius R, and we need 1 more eqn to solve this. At this point, Bohr postulated that angular momentum of electron can't be continuous value, and can only take discrete values, i.e mvR = n*h, where h=planck's constant, and n=0,1,2,3,... There were no physics involved in this assumption, nor did he know why it would take only discrete values.
However 10 years later, De Broglie figured out the real reason. Electrons are both particle and wave. For a wave to form constructively in a Radius R, the distance 2*pi*R can only take values of λ, 2λ, 3λ, .. etc. Only then can standing waves be formed in that distance. De Broglie wavelength is also defined as λ=h/p where p=momentum=m*v, h=planck's constant.
Link: https://phys.libretexts.org/Bookshelves/College_Physics/Book%3A_College_Physics_1e_(OpenStax)/30%3A_Atomic_Physics/30.06%3A_The_Wave_Nature_of_Matter_Causes_Quantization
This yields: 2*pi*R=n*h/(m*v), or mvR=h/2*pi => Eqn (2) same as Bohr's postulate for angular momentum.
Using this 2nd Eqn along with 1st Eqn, we can solve for R. Use v=h/(2*pi*m*R) from 2nd Eqn and substitute in 1st. We get R=n^2*a0 where a0 is the radius of 1st shell for n=1, a0 = (h/2*pi)^2/(m*e^2) = 0.5Å. Angstrom is the unit that is used for size of atoms, as that's the order of size for most of the atoms. An Angstrom is 1/10 of a nm.
Size of atoms:
How does the size vary for larger atoms? For Helium, we have 2 proton and 2 electron. Since the 2nd electron is also in n=1 shell, the radius of atoms doesn't increase, but at the same time, the force b/w the electrons and protons is doubles, since there is charge=+2(e) on 2 protons. So, we would expect size of Helium atom to be smaller. In fact, since going across the periodic table in a given row, the largest shell number remains same, it implies that sizes should decrease, as we get more protons attracting the electrons. This is what we see in reality. Going from 1st group to 18th group, size decreases to almost 1/3.
Also, as we move down the table, sizes should increase as an extra shell gets added. However, at the same time more protons are also getting added, resulting in greater attraction. There's also a shielding effect, that shields outer shell electrons from full charge of nucleus being seen (as inner shell electrons can be considered as part of nucleus, hence effective charge is lowered by the number of electrons). As a result of these 2 opposing effects, we can consider charge remaining almost same as we add extra shells. So sizes end up increasing solely due to extra shell being added. Going from n=1 to n=2, size increases by 3X, but going from n=2 to larger shells, size increases are more modest at 20% per shell added.
In reality, radius of these orbits is not well defined. electrons have a probability cloud around the nucleus, and can be found anywhere, not at a definite radius. So, it's hard to define what is the size of atom. Below link explains various ways, size of atoms are defined and measured.
Size of atoms: https://chem.libretexts.org/Courses/Howard_University/General_Chemistry%3A_An_Atoms_First_Approach/Unit_1%3A__Atomic_Structure/Chapter_3%3A__The_Periodic_Table/Chapter_3.2%3A_Sizes_of_Atoms_and_Ions
Size of Hydrogen is about 50pm=0.5A, while largest element in 6th row has size=300pm=3A. For most of the atoms, size lies in between 1A and 2A, except for atoms in top right and bottom left of the periodic table.
Ionization energy (IE):
We can solve for Energy for any shell (n) as En = -13.6eV/n^2 where n=1,2,3...
So, energy increases (becomes less -ve) as n increases. Electrons can move from n=1 to n=2 by absorbing energy (from light waves). If enough energy is supplied, electrons may jump to very large "n" shell, which is effectively close to "0" energy. "0" energy implies that electrons and protons are at infinite distance with no attraction b/w them, i.e no force to hold them together, at which point electrons are free to move out from the atom and wander anywhere. So, 13.6eV is the energy needed to free the electron, or in other terms, ionize the Hydrogen atom. You have to supply that energy via some light wave which is absorbed by the atom and frees the electron. This is known as the IE for1st electron to ionize H to H+.
This Bohr's theory explained why each element had it's unique spectral lines. However, it didn't talk about sub-shells s, p, d ,f and so his formula assumed same energy for all electrons in a given shell (which is incorrect).
Energy of any EM wave for a given frequency = h*ν where h=planck's constant, ν=frequency of wave. So, as freq of EM wave goes up, energy goes up. That's why X-ray, Gamma ray are considered harmful to human body, as they have very high freq, resulting in higher energy which can damage human cells.
Energy (in eV) = h*c/λ = 1240 eV-nm / (λ in nm) => Energy of a photon in visible light wave (λ=700nm to λ=400nm) = 2eV - 3eV
To convert eV to Joules, we can use defn of Joules which is defined as 1J=1N-m. When 1 coulomb charge moves thru Electric field of 1V/m, then work of 1J is performed. So, 1J=1Coulomb*1V
1 electron's charge = 1.6*10^-19C => 1eV = 1.6*10^-19C*1V = 1.6*10^-19J. => 1eV = 1.6*10^-19J
For any element's atom to absorb or emit photon, it's electron has to move from 1 energy state to another energy state. Since energy states are discrete based on En = -13.6eV/n^2, it implies that
h*ν= -13.6eV*(1/n1^2 - 1/n2^2) where n1 and n2 are two energy states where the electron jumps from/to, and ν is the frequency of wave emitted or absorbed. This matched exactly with the spectral lines observed for Hydrogen atom.
Below link shows how spectral line can be calculated based on energy of electrons jumping from 1 shell to another: https://chem.libretexts.org/Courses/University_of_Arkansas_Little_Rock/Chem_1402%3A_General_Chemistry_1_(Belford)/Text/6%3A_The_Structure_of_Atoms/6.3%3A_Atomic_Line_Spectra_and_Niels_Bohr
Ionization energy is usually expressed in J/mole (defn of mole is explained later below). Energy of 1 electron moving under Voltage 1V = 1 eV =1.6*10^-19J. 1 mole = 6.02*10^23 electrons, so energy = 6.02*1.6*10^4J=96.3KJ/mole.
So, 1eV/atom = 96.3KJ/mole.
IE of H->H+ is = 13.6eV = 13.6*96.3=1310 KJ/mole. This is what we see in the IE table of elements in link below for Hydrogen.
IE Concepts => https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/07%3A_Periodic_Properties_of_the_Elements/7.04%3A_Ionization_Energy
However, as we move to other elements, Bohr's simplistic model no longer works for IE. For next element Helium, the Ionization energy is lot higher at 2400 KJ/mole as He has full shell (1s2) . Same is the case with other noble gases. As we go down the periodic Table, IE goes down as electrons are in shells further away from the nucleus, so less energy is required to free that electron. As we move across a row from left to right, IE increases since effective nuclear charge increases, as well as the radius is smaller due to electrons being pulled closer in.
What we see until now is called the First IE, as it's the very 1st electron that's removed to give the atom a +ve charge. If we remove the 2nd electron, it's called the 2nd IE, and so on for 3rd IE, 4th IE, etc. As expected IE1 < IE2 < IE3 .... as nucleus is already +vely charged after the removal of 1st electron, so removing electron from more +ve species takes more energy. On top of this, if we hit a full shell, and next electron is to be removed from completely full shell, then 10X more energy is required. This excessive energy is not available in chemical reactions, that's why we see atoms losing electrons only upto when they hit the full shell.
IE of diatomic molecules like H2 , O2 , N2 etc is usually higher compared to their atomic parts as energy of molecule is lower (as covalent bond formed more strongly ties the electron to proton), IE1 of H2 is 1488 kJ/mole, while IE1 of single H atom was 1310 kJ/mole. IE2 for H2 is higher than IE1, but is not directly measurable, as H2+ is highly unstable and readily breaks into individual protons. Below link shows IE for few diatomic atoms.
IE of diatomic molecules => https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Atomic_Theory/Ionization_Energies_of_Diatomic_Molecule
Interestingly, we see that IE of F Molecule is lower than that of F atom. There are many such cases, so we need to develop theory of hybrid orbitals.
Bond Energy (BE)
For atoms, total energy is the energy required to break apart the atom into nucleus (protons+neutrons still intact) and individual electrons. For molecules, this total energy isn't that meaningful, as we are not interested in disassociating molecule into "nucleus" and individual electrons. Rather we are only interested in to breaking that bond and forming individual atoms with their electrons intact. i.e If we are forming H2O from H2 and O2 , we are interested into energy required to break apart H2O into H2 and O2 . This is known as bond energy or bond dissociation energy, and it reflects the energy present in that bond. If we are further interested in bond energy or H molecule or O molecule, then we break apart H2 and O2 into H and O atoms. Bond energy is totally different than IE.
When a molecule forms from individual atoms, usually some energy is released as the total energy of the molecule is lower than the sum of energies of it's atoms. This is because the formation of a molecule itself implies that energy would be lower for the molecule, hence the reason the molecule formation took place. Or seen from other perspective, the bond will require energy to break it, hence energy was released when forming it, implying lower energy of the molecule. Such reactions are called exothermic reaction which are chemical reaction that release energy (so the total energy of the newly formed compound is lower). In contrast the opposite reaction, where the compound is broken into individual atoms needs energy to break the bond, and is called endothermic reaction. For some compounds, even the forming of compounds from it's constituent atoms may need energy or breaking it may release energy. When few compounds react to form few other different compiunds, then it's hard to say whether energy is released or absorbed. It depends on the amount of bond energy present in each compound in the reactants as well as in the final products. We'll discuss how to find that in a separate section later.
Bond dissociation energy of H2 molecule is 436KJ/mole.
H2 (+Energy) -> H + H (this requires 436KJ/mole of energy for this reaction to happen). This is endothermic reaction
H + H -> H2 (+Energy) (this releases 436KJ/mole of energy when this reaction happens, no external energy is required). This is exoothermic reaction
So, the total energy of H2 molecule is energy of each H atom + energy released. Energy of single H atom is -1310KJ/mole, so 2 H atoms have -2620KJ/mole (or -1310 KJ for half the mole, since 2H atoms combine into one molecule as H2. However, formation of H2 molecule releases 436KJ/mole energy as the bond formed is lower in energy. So, energy of H2 molecule is = -2620 - 436 = -3056 KJ/mole.
Molecules with triple bond have higher BE than those with double bond, which in turn have higher BE than molecule with single bond. BE of most common bonds shown below.
BE link => https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Chemical_Bonding/Fundamentals_of_Chemical_Bonding/Bond_Energies
Bond length (BL) in molecules:
Bond length in molecules basically determines the size of the molecules. The closer the individual atoms are when forming the bond, the smaller the molecule size. The length of the bond is determined by the distance where the minimum potential energy occurs for the bond. As an example, for Hydrogen, the 2 atoms at far off distance have 0 PE. As they come closer PE keeps on going down, until it reaches a minima of -436KJ/mole. That is the distance, 74 pm, where the bond is formed, and is called the Bond Length. AS we start getting closer, the PE again starts increasing, and even goes above 0, for very close distances.
Bond order: Bond order refers to the number of bonds formed b/w 2 atoms (see in Bonds section), Double or triple bond are stronger than single bond, and hence require more energy to break them, implying PE of bonds goes lower as the bond order increases. So, N2 which has triple bonds has lower PE and shorter BL, then O2 which has double bonds, and
Vid (KA) => https://www.khanacademy.org/science/ap-chemistry-beta/x2eef969c74e0d802:molecular-and-ionic-compound-structure-and-properties
Lattice Energy: Compounds like NaCl form a lattice kind of structure with alternating Na and Cl atoms held together via ionic bond. Energy required to break this lattice to separate out the ions is called lattice energy.
Energy bands:
We saw above that isolated Hydrogen atom will have energy levels as -13.6eV, -13.6/4eV, etc. However, when 2 of such Hydrogen atoms come close together, they start interacting and affecting the fields. As such 1s, 2s, 2p energy levels from different atoms cannot co-exist due to Pauli's exclusion principle. It states that no 2 electrons can occupy the same energy level. In response, these energy levels split into 2 => So, 1s will split into 1s(low) and 1s(high) energy levels. When we have 4 atoms, they will split into 4 very closely spaced levels. For large number of N atoms, these levels will split into N levels, which forms a band. For atoms with multiple orbitals, the outermost orbitals split more than the inner ones. When large number of atoms are brought together in forming a solid, there are so many levels from splitting, that a continuous band of energy is formed. Within this continuum of energy band, there are some regions called as "forbidden energy band" or "band gaps" where no orbitals exist no matter what the temperature is. These band gaps and their widths are determined from the nature of the atoms. Explained below:
Energy bands => https://eng.libretexts.org/Bookshelves/Materials_Science/Supplemental_Modules_(Materials_Science)/Electronic_Properties/Energy_bands_in_solids_and_their_calculations
Thermal and Electrical conducting properties of solids are determined from these Energy Bands. The topmost band with completely filled electrons is called valence band (VB) (since it's filled with valence or outer shell electrons) while the band right above it is called conduction band (CB). Conduction band may be partially or not filled. Number of electrons in Conduction band determine the conductivity of that element. If the conduction band is empty to start with, and if somehow thru thermal excitation, electrons can be made to jump to this band, then that material will start conducting. This gives rise to metals, nonmetals and SemiC.
Supplement (along with sim) => https://eng.libretexts.org/Bookshelves/Materials_Science/Supplemental_Modules_(Materials_Science)/Electronic_Properties/Energy_bands_in_solids_and_their_calculations
- In Metals, valence band and conduction band overlap each other. VB is filled with electrons while CB always has empty states. In presence of Electric field, VB electrons jump to CB causing it to conduct.
- In Insulators, valence band and conduction band are separated by large energy gap of several eV. Electrons from VB can't get excited enough to jump to CB, and hence no conductivity.
- In SemiC, the bandgap is smaller at 1eV, and so with enough Electric field, electrons can get excited to jump to CB, and hence starts conducting a little. Except for this BG difference, SemiC are similar to Insulators.
Fermi Level:
The energy band in the materials is filled with electrons based on a Fermi Dirac distribution curve. This gives the probability of finding an electron at Energy level E, and at Temperature T. using this, we can find the exact distribution of electrons in any energy band. Fermi Energy level (EF) is a hypothetical level within this band, where the probability of finding an electron is 50%. More the electrons above this Fermi level, more the electrons in CB and higher the conductivity. As Temp inc, more and more electrons occupy higher Energy band, and hence are in CB, and start conducting even more. However, as we see in the section on R,L,C, conductivity is determined both by number of electrons in CB as well as the mobility of electrons. In metals, inc in number of electrons in CB is almost negligible with Temp, as most of the electrons are already in CB. However, mobility decreases resulting in lower conductivity. With SemiC, situation changes as exponentially more electrons move into CB with inc temperature. Mobility still decreases but only as i/T^2 while electron conc in CB goes exponentially. So, conductivity of insulators and SemiC increase exponentially with inc in Temp.
Link => https://eng.libretexts.org/Bookshelves/Materials_Science/Supplemental_Modules_(Materials_Science)/Electronic_Properties/Fermi_Energy_and_Fermi_Surface
Mole and Avagadro Number:
Since the number of atoms is very large even in small amounts of any element, we need to come up with a unit for number of atoms. Mole is such a unit. It's the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of "carbon-12 12
6C
". We take 12 g of 12
6C
in the defn of mole, but we could have easily taken 1g of "Hydrogen-1 1
1H
" in the defn. 1 atom of "Carbon-12" has 12 amu of weight, while 1 atom of "Hydrogen-1" has 1 amu of weight.
So, 12g of C-12 has = 12g/12amu = 1g/1amu atoms, while 1g of H-1 has 1g/1amu atoms. So, all these elements have same number of atoms for a weight that is normalized depending on how many amu of weight each atoms has for that element compared to H-1 atom. To keep it simple, we say 1 mole is the number of atoms in 1 g of H-1 (or 12g of C-12 to be precise). It turns out 1 mole = 6.02*10^23 (approx), and that is the number of atoms in 1g of Hydrogen. This is also the number of atoms in 4g of He (since each He atom is 4 amu), and 16g of Oxygen (since each Oxygen atom is 16 amu).
The exact number 6.02214076 * 10^23 is also known as "Avagadro number" or "No". The exact number of atoms in a given mass of an element is impossible to determine, since it will vary considerably depending on the shape, crystalline structure, purity, temperature, pressure, etc. However, for sake of definition, we chose this somewhat arbitrary number to 8 decimal places as our reference number for "Avagadro Number".
