Details

Published: Sunday, 15 June 2025 14:46

Hits: 435

Roofing Repair : DIY

Roofing just like AC is one of the other dreaded DIY job. It's very expensive to repair (roofs costing > $20K to replace, usually $50K or so to get a good roof). Again you are dependent on the contractor to do a good job, and it's big money. A lot of companies may charge you less, but do shabby work with low quality material. You can never go just based on price. Also, there is no way to know the kind of work that the Roofing Company did.  Just like a AC repair, you will come to know about the quality of their work few years down the line.

There are lot of scalpers who will go home to home advertising "free roof inspections", and will immediately point to a lot of hail damage and other damages to the roof. Even for newly built houses, they will find "roof damage" and insist on fling a claim with your insurance. They will also say that they will cover your deductible, so that your out of pocket cost for replacing the roof is going to be $0. I never believe these guys. Most of the times, insurance won't even approve the replacement of roof. May be these scalpers are able to have a 10% success rate, but that's good enough for their business. Also, since they aren't charging you any money,  they will have to resort lowest quality material and shabby workmanship to still make a profit. Roof is an expensive repair, and if you aren't careful, ou might end up with a roof, which is worse than what was there before :(

Repairing a singlr damaged shingle: Remeber that shingles are put in overlapping layers, where one 3 ft shingle has 2 shingles on top in a layerd fashion. We have 4-6 nails on our damaged shingle right under the first shingle on top of it, and then another 4-6 nails on our damaged shingle right under the second shingle on top of it. Only when we remove both layers of nails (Total 8-12 nails), we can remove the damaged shingle.

Vid on replacing single architectural shingle => https://www.youtube.com/watch?v=O1lXsXM2E4c

Details

Published: Tuesday, 03 June 2025 01:29

Hits: 609

Calculus:

We'll start with limits and then move to differentials and integrals.

Nice cheat sheet showing all imp Calculus formulas => https://math.colorado.edu/math2300/resources/calc1/lamar/Calculus_Cheat_Sheet_All.pdf

Limits:

Limits are one of the easiest to master. They form the basis of calculus. When we say limit, we are trying to find the value of a function, as it approaches a particular value of a variable.

ex; Y= 2*x+5. This is a straight line, and when I say what is the value of Y at x=3, it's 2*3+5=11. No if I say, what's valve of Y as x approaches 3 from left side of graph (denoted as -> 3-), or from right side of graph (denoted as -> 3+), it's still 11. So, most of the cases limit is as simple just substituting the value.

In some, the exact value of the Func doesn't exist at that point, but in this case, limit may still exist, since Limit says it approaches that value, but is never exactly that value.

ex: Y = (x^2-4)/(x-2). Here at x=2, the function is 0/0 which is undefined. However, we can write it as Y=(x-2)(x+2)/(x-2). If x≠2, then we can cancel out (x-2) from top and bottom, and func Y=(x+2). Now as x->2 (from left or right, doesn't matter), the value is 4. However, at exactly x=2, the value doesn't exist (you mark it as a open dot instead of a filled in dot). Since the value of limit (=4) is same both from left and right, we say that the limit exists, even though the limits don't give the same value of 4 at x=2, i.e Y(x=2)≠4.

When evaluating limits, Func which yield values as 0/0, ∞/∞, 0*∞ are all undefined, and hence you have to either cancel out some term, or rewrite the expression so that it can be evaluated to a known value on substitution (and NOT yield undefined values). Most of the complicated function limits are evaluated by expanding the complex function as Taylor series (i.e as polynomial function). Then something usually cancels out leading to a limit value.

Some well known limits are:

• Lt x->0 (sin(x))/x = 1 (write sin(x) as Taylor series and cancel out x from numerator and denominator). It's 0/0, but evaluates to 1 in limiting case. On Khan academy, proof of this is provided using other limit theorem (sandwich theorem of limits), which finds the limit of 2 other functions, and sandwiches this func b/w those 2 func. Since the limit of other 2 func approaches 1, the limit of this func will also need to be 1.
• Lt x->0  (1-cos(x))/x = 0 (expand using Taylor series).  It's 0/0, but evaluates to 0 in limiting case (unlike sin case above which evaluates to 1).
• Lt x->∞  (1+1/x)^x = e. Here inside term goes to 0 while exponent term goes to ∞, so hard to see it can approach a particular value as e. Can be proved by doing "Binomial Thm (BT)" expansion of series, or by taking log of this func, and then using limit of log. One such proof using BT => https://www.mathdoubts.com/lim-1-plus-1-by-x-whole-power-x-as-x-approaches-infinity-proof/
• More limits => https://planetmath.org/ListOfCommonLimits

ex: Limit of sin(x))/x can easily be found by using L'Hôpital's Rule. Lt x->0 (sin(x))/x = Lt x->0 (cos(x))/1 = 1/1 = 1.  

Differentiation (Derivatives):

Differentiation follows from limits. A derivative of a function is the slope of a function at every point of the function. The slope at a point is defined as a line that touches the function at only 1 point (i.e a tangent at that point). This slope itself may be another function, and it's denoted as f´(x) (i.e f with a prime on top).

Avg slope of a function b/w any 2 points x1 and x2 is = [f(x2)-f(x1)] / (x2-x1). Now if we start getting x2 closer to x1, then avg slope we get is for a narrower section of the function. If we make x2 infinitesimally close to x1, then, in the limiting case, we get the slope of the function at the point x1.

Let's rewrite x2 as x2=x1+Δx, then slope = [f(x1+Δx) - f(x)] / Δx

So,  f´(x) = Lt Δx->0  [f(x+Δx) - f(x)] / Δx => The eqn we get for derivative is the function that shows the slope of f(x) at any point x. The limit has to exist from both left and right side and be the same, only then f´(x) exists and it's value is the common value. Only in this case is the function f(x) said to be differentiable.

Conditions for differentiability at a point c:

• Func needs to be continuous at point c (in this case, limit will be same on both sides of point c, and equal the value of func at c, i,e f(x=c) = Limits from both left and right.
• Func needs to have same slope on both sides (i.e no sharp turns or infinite slope).

Conditions for differentiability (with nice examples) => https://math.libretexts.org/Courses/Irvine_Valley_College/Math_3AC%3A_Analytic_Geometry_and_Calculus_I/07%3A_Derivatives/7.04%3A__Differentiability

ex: f(x)=x^2, find f´(x). Here we find derivative using the defn above. 

f´(x) = Lt Δx->0  [f(x+Δx) - f(x)] / Δx = Lt Δx->0  [(x+Δx)^2 - x^2] / Δx = Lt Δx->0  [2.x.Δx + Δx^2]/Δx = Lt Δx->0  [Δx(2.x+Δx)] / Δx = Lt Δx->0 2.x+Δx = 2.x

So, slope of function x^2 is 2.x at any point x. We can verify this by drawing slopes at x=1, x=2, x=4, etc and confirm that the slope is indeed 2, 4, 8, which is 2.x !!

Similarly derivatives can be found for many common functions. In most cases, we have to do a Taylor series expansion to cancel out  Δx in both numerator and denominator.

f(x)=sin(x). To find f´(x), we expand sin(x) as Taylor series,, cancel out Δx, and the series left is cos(x). So, f´(x) = cos(x)

If f(x)=cos(x), then f'(x) = -sin(x)

Cheat sheet => https://tutorial.math.lamar.edu/pdf/calculus_cheat_sheet_derivatives.pdf

Derivative Rules:

• Constant Multiple Rule: d/dx[k*f(x)] = k* d/dx(f(x)), where k is a constant.
• Power rule: d/dx(x^n) = n*x^(n-1). Most widely used to differentiate polynomials. Any continuous function can be written as a polynomial, so individual terms of the polynomial can be differentiated using this formula. If we keep on differentiating poly of x^n n times, then it will keep reducing the power of poly func by 1 each time, and ultimately the result would be 0.
• Sum/Difference Rule: d/dx [f(x) + g(x)] dx = d/dx[f(x)] +  d/dx[g(x)] (instead of +, we can have - too)
• Product rule: d/dx [f(x).g(x)] = g(x).d/dx(f(x) + f(x).d/dx(g(x) => basically you differentiate each function separately and multiply it with the undifferentiated func.
• Quotient Rule: d/dx [f(x)/g(x)] = g(x).d/dx(f(x) - f(x).d/dx(g(x) / [g(x)]^2. This can be derived from product rule as g(x) can be replaced with 1/g(x). Then d/dx(1/g(x)) = -1/[g(x)]^2 * d/dx(g(x)) and we get the quotient rule.
• Chain Rule: Written in 2 forms:
  • d/dx [f(g(x))] = d/d(g(x)) [f(g(x))] * d/dx(g(x)) => NOTE: the 1st derivative is wrt g(x) and NOT x. You may substitute g(x) with var "u". That is the form that the 2nd form of chain rule is written in as shown below.
  • dy/dx = dy/du * du/dx where y may be written as a func of var u. 

Some common derivatives:

Link for common derivatives and rules => https://www.mathsisfun.com/calculus/derivatives-rules.html

• d/dx(e^x) = e^x (drive from defn of derivative, and then using series expansion of e^x). 
• d/dx (a^x) = ln(a). a^x. We can derive this from differentiation of e^x. a^x can be rewritten as e^(x ln(a)). This is because if we take natural log of both sides, then ln(a^x) = ln (e^(x ln(a)) => x (ln a) = x (ln a), so both sides become equal. Now d/dx(a^x) = d/dx(e^x(ln a) = e^(x(ln a)) . d/dx(x * ln(a)) = ln (a). e^(x(ln a) = ln(a). a^x.
• d/dx(ln x) = 1/x . Since ln (x) is inverse fn of e^x, we can use above derivative of e^x to find this one. Let y=ln(x) => x=e^y, => d/dx(x) = d/dx(e^y) => 1 = d/dy(e^y).dy/dx => 1=e^y.dy/dx => dy/dx = 1/e^y = 1/x  .
  • NOTE: ln (x) is only defined for x>0. This will be important in integral (discussed below) as If we want to have  ∫ 1/x = ln(x) only for x>0. If x<0 in limits, then we can only do integral only if we take mod x, i.e ln |x|. So  ∫ 1/x = ln(|x|) if we want to be exact. This ensures that just as 1/x graph exists in 1st and 3rd quadrant, ln(x) exists in all 4 quadrants for all values of x.
• d/dx(log_ax) = d/dx(ln(x)/ln(a)) = 1/(x.ln(a)).
• Trignometric func: Differentiation of Trignometric functions require using the limit theorems for basic func as sin(x). Others can be derived using this differentiation.
  • Regular trig func: sin, cos, etc
    • sin(x) or cos(x) =>  derivative of cos(x) has -ve sign.
      • sin(x): d/dx(sin(x)) = cos(x). Use basic limits as sin(Δx)/Δx =1, and [(1-cos(Δx)]/Δx =0 as Δx approaches 0 to prove the sin(x) derivative. Others follow. 
      • cos(x): d/dx(cos(x)) = -sin(x). NOTE the -ve sign in derivative.
    • cosec(x) or sec(x) =>derivatives that give sin(x) or similar form have -ve sign in final result. So, csc(x) gives -ve sign when differentiating.
      • csc(x): d/dx(cosec(x)) = d/dx(1/sin(x)) = [-1/sin²(x)].cos(x) = -cosec(x).cot(x). NOTE the -ve sign in derivative.
      • sec(x): Similarly d/dx(sec(x)) = d/dx(1/cos(x)) = [-1/cos²(x)].[-sin(x)] = sec(x).tan(x). NO -ve sign.
    • tan(x) or cot(x):
      • tan(x) => d/dx(tan(x)) = d/dx((sin(x)/cos(x)). Using quotient rule, we get f'(x)= sec²(x)=1/cos²(x)
      • cot(x) => d/dx(cot(x)) = d/dx((cos(x)/sin(x)). Using quotient rule, we get f'(x)= -cosec²(x) = -1/sin²(x). Or other way is by using d/dx(1/f(x)) where f(x)=tan(x). So, d/dx(1/tan(x)) = -1/tan²(x).d/dx(tan(x)) = -1/tan²(x).(1/cos²(x)) = -1/sin²(x). NOTE the -ve sign in derivative.
  • Inverse trig func: These are written as sin^-1(x) or arcsin(x). For each pair below, the derivative of other inverse func is just a -ve of the other one, so easy to remember.
    • sin^-1(x) or cos^-1(x) => We let sin^-1(x) = y => sin(y) =x => cos(y).dy/dx = 1 => dy/dx= 1/cos(y) = 1/[√(1-sin²(y)] = 1/( √(1-x²). Similarly  d/dx(cos^-1(x)) = -1/sin(y) = -1/[√(1-sin²(y)] = -1/( √(1-x²) (we just add a -ve sign for this). In these x≠+/-1, as that will yield ∞.
    • tan^-1(x) or cot^-1(x) => We let tan^-1(x) = y => tan(y) =x => sec²(y).dy/dx = 1 => dy/dx = 1/ sec²(y) = cos²(y) = 1/(1+x²). Similarly d/dx (cot^-1(x)) =  -1/(1+x²) (we just add a -ve sign for this)
    • csc^-1(x) or sec^-1(x) =>These are less used. We can use similar techniques. d/dx (sec^-1(x)) = 1/[|x|.√(x²-1)]. Similarly d/dx (csc^-1(x)) = -1/[|x|.√(x²-1)] (we just add a -ve sign for this). In these x≠+/-1, as that will yield ∞. Also, we have to do |x| as without modulus, the slope is incorrect for -ve values of x, so we do |x| to make it correct for both +ve and -ve values of x. One such proof here: https://math.libretexts.org/Bookshelves/Calculus/Supplemental_Modules_(Calculus)/Differential_Calculus/Differential_Calculus_(Seeburger)/Derivatives_of_the_Inverse_Trigonometric_Functions

Tricky differentiation using above rules:

• ex: d/dx(x^x). Take y=x^x => ln(y)=xln(x) => d/dx(ln(y)) = d/dx(xln(x)) => 1/y*dy/dx=ln(x) + 1 => dy/dx=y[1+ln(x)] =>  d/dx(x^x) = x^x * [1+ln(x)] 

Derivative of inverse functions:

If we have f(x) and it's inverse  g(x)=f^-1(x), then if slope of f(x) = m at pt (x1,y1), then slope of g(x) will always be 1/m. Reason being that inverse function is just y replaced by x (and x replaced by y). So if original func f(x) had slope m=Δy/Δx, then it's inverse func g(x) will have slope Δx/Δy (as x and y are interchanged for inverse func), which is = 1/m. So, the g´(x) = 1/f´(x). The only point to watch out is that if the slope of original func f(x) was at point (x1,y1), then the inverted slope is at point (y1,x1) as the x,y coordinates get interchanged. So if f(x) slope is m at (b,a), then g(x) slope will be 1/m at (a,b). => a=f(b) => b=f^-1(a) 

g´(x=a) = 1/f´(x=b) => g´(x=a) = 1/f´(x=b) => g´(x=a) = 1/f´(g(x=a)) = 1/f´(f^-1(x=a)) [since g(x) = f^-1(x))]

ex: f(x)=x^2, then g(x)=f^-1(x)=√x 

f´(x)=2x, g´(x)=1/(2x), At x=3, f´(x)=2x=6 (at coord (3,9)), so g´(x)=1/(2x) = 1/6 at coord (9,3). NOTE: the coordinates chaged. If we want to find g´(x=3) (i.e coord (3,√3)), then we need to find f´(x=√3) = 2√3 => g´(x=3) = 1(2√3)

We can also use above formula directly:  g´(x=a) = 1/f´(g(x=a)) => Since g(x=3) = √3, g´(x=3) = 1/2x @x=√3 = 1(2√3), which is same as what we obtained above.

Maxima/Minima:

Derivatives can be used to find maxima and minima if functions. This is one of the most used application of derivatives in real life.

KA: https://www.khanacademy.org/math/ap-calculus-bc/bc-diff-analytical-applications-new/bc-5-8

Following defn used to describe shapes of func when dealing with max/min: NOTE: A "down func" implies real func, while "up func" implies opposite of the real func behaviour. For ex: both "convex" or "convex down" imply a rice bowl kept on table, which is how "convex" func are defined. However a "convex up" func implies the opposite behaviour, i.e  a rice bowl kept upside down on table.

• Convex func: (aka Concave upward or convex downward): Any func whose slope increases is convex or concave up (like a rice bowl kept on table), i.e slope goes from -ve to 0 to +ve or any part where slope is increasing. 
• Concave func (aka concave downward or convex upward): Any func whose slope decreases is concave or convex up (like a rice bowl kept upside down on table), i.e slope goes from +ve to 0 to -ve or any part where slope is decreasing.
• Infection point: This is the point where the func changes from convex to concave or vice versa.

A continuous and smooth function (most of the real functions are smooth, an exception is absolute value func) will have it's slope=0 at maxima and minima. These are local max/min, as many of these local max/min may exist. There's no way known to find the absolute max/min of any func. Over a limited domain of x values (i.e x goes from x1 to x2), we can determine absolute max/min by looking at all points where slope is 0, undefined or at end points. Whether the point is maxima or minima is determined by 2nd derivative.

• 1st derivative: Given f(x), find first derivative f'(x). If f'(x) =0 at x=x1, it's either a maxima, a minima or a infection point. An infection point is a point where slope is 0, but instead of reversing direction (i.e slope), it keeps on moving in same direction.
•  2nd derivative: Now find 2nd derivative f''(x) at x=x1. Depending on 2nd derivative sign, we can determine whether it's max or min
  • Maxima: If f''(x1) < 0, then x1 is a point of local maxima. This is because, at maxima, it's concave, so slope of this func goes from +ve to -ve (decreasing). Then, derivative of this slope (i.e f''(x)) will be -ve. If you don't want to check for 2nd derivative, then you can also check sign of first derivative, f'(x). If f'(x) changes sign from +ve to -ve when going thru x1, then it's a maxima.
  • Minima:  If f''(x1) > 0, then x1 is a point of local minima. This is because, at minima, it's convex, so slope of this func goes from -ve to +ve (increasing). Then, derivative of this slope (i.e f''(x)) will be +ve.  If you don't want to check for 2nd derivative, then you can also check sign of first derivative, f'(x). If f'(x) changes sign from -ve to +ve when going thru x1, then it's a minima.
  • Infection point: Here, func changes from convex to concave or vice versa, implying f''(x) changes sign from +ve to -ve or vice versa. Basically f''(x)=0 at point of infection (as sign change can only happen when it passes thru 0). At infection point, slope of the original func, f(x), may or may not be 0 (i.e f'(x)=0 or f'(x)≠0). 
    • If f'x(0)=0 and f''(x)=0, then func continues going in same dirn after hitting a flat portion. No max or min exists, though slope of f(x) does go to 0
    • If f'x(0)≠0 and f''(x)=0, then func is changing shape from convex to concave or vice versa. No max or min exists as slope of f(x) never goes to 0

Plotting functions: Complicated functions can be plotted by utilizing calculus. We find derivatives to find out where the slope is 0 or undefined, as well as the regions of increasing/decreasing value, which helps us plot it. 3 different kinf of func really easy to plot using calculus. See in KA for these examples: 

• Polynomial functions: Ex: f(x)= 3x^4-4x^3+2. f'(x) =0 at x=0,1. Now, we find  f''(0) and f''(1). If it's > 0, then it's min, else it's max. At x=0, f''(0)=0, implying it's infection point, so slope remains same. to find whether func is inc or dec. 
• Log function: Ex: f(x)=

Integration (Integral):

Integration is inverse of differentiation. Integral is the inverse function of derivative. We denote it as ∫ f(x). Given function f(x), if  F´(x) = f(x), then ∫ f(x) = F(x). F(x) (denoted with capital F) is the inverse func of f(x). See Inverse function in other sections.

F(x) -> differentiate -> f(x).  F´(x) = f(x),

F(x) <- integrate <- f(x). F(x) = ∫ f(x).

Integration was originally developed as "finding area under curve". Later Barlow and Toricelli in 17th century found hints of connection b/w differentiation and integral. Barrow provided the 1st proof of "fundamental Thm of Calculus". Later Newton and Leibniz did more advanced work on calculus, where integral was found to be inverse function of differentiation, which made it easy to solve integral

But why is integration area under a curve? Let's say A(x) is some function of f(x). At x=x1, A(x) is A(x1). Now, if we take incremental "dx" at x=x1, and compute f(x).dx, then f(x).dx gives area of the incremental rectangle formed. So, incremental increase in area is f(x).dx. So, A(x) must be the area of the function, as incremental area dA(x)=f(x).dx => dA(x)/dx = f(x). Or A(x) =   ∫ f(x).dx

This vid shows it formally by using MVT => https://www.youtube.com/watch?v=U3u0PF7n-xg

Integration is usually taught as avg value of a continuous func. To make it easier, we divide f(x) into N discrete sections and then find avg value.

Then avg = [∑f(x) ] / N, where summation is over N points, and each point is spaced apart by dx, so no. of points N = (b-a)/dx. So, area =  Avg height of f(x) * base = [∑f(x) ] / (b-a) * dx * (b-a) =  [∑f(x) ] * dx where a,b are endpoints on x axis

Now if we start taking limit dx->0, then avg value of this func approaches closer to it's real value. So, Area = Limit dx->0  [∑f(x) ] * dx =  ^b
_a∫ f(x).dx

Fundamental Thm of Calculus:  ^b
_a∫ f(x).dx = F(b) - F(a) where  F´(x) = f(x). There are 2 parts of this Thm, but they are almost same, I'm writing both parts as one (strictly there are 2 parts). What's insane is that the area of the whole curve can be found by just looking at the values of antiderivative at the endpoints o the curve !! We'll see why that happens below. 

Essence of Calculus explaining Integration as area under curve => https://www.3blue1brown.com/lessons/integration

We learn integration as the area under the curve. However, the function that we get via integration F(x) is actually the inverse function of f(x), i.e F´(x) = f(x). But differentiation gives the slope, while it's inverse func gives the area. How is the slope and area related? This fundamental question is explained nicely here => https://www.3blue1brown.com/lessons/area-and-slope

To see this relationship, 2 key points to observe:

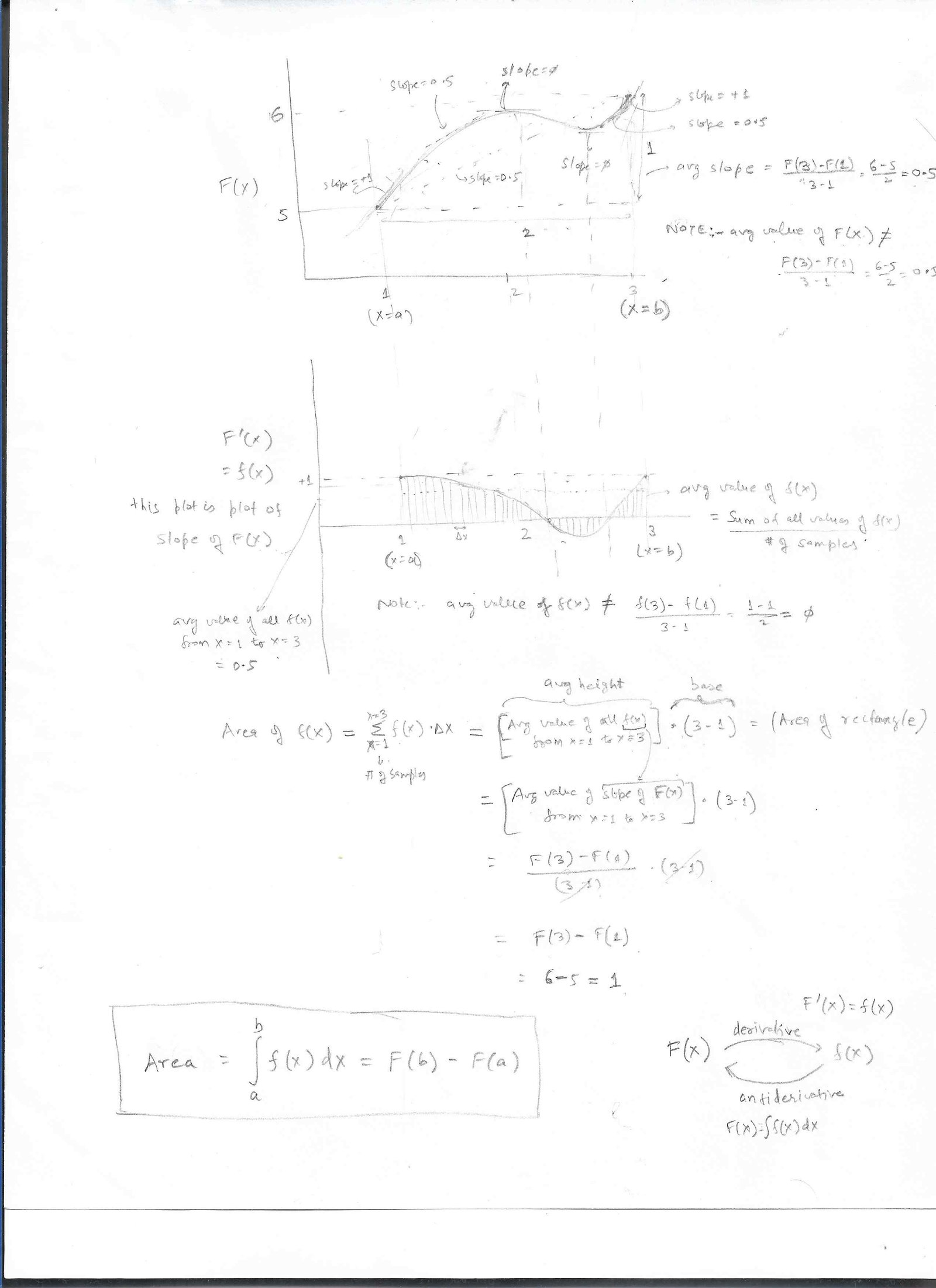
1. Avg slope for any func can be calculated by just looking at End Points: If you were given a bunch of numbers in any order, would you be able to calculate it's avg just by looking at 1st and last number? Answer is => NO. You won't be as the avg is decided by all the numbers. Now consider continuous plot of such numbers. Again, it's the same thing => you won't be able to calculate the avg of this continuous func, just by looking at the 2 endpoints of the curve. But now, let's say, I calculate the slope of this function, and plot this new function which is the slope of our original function at every point of the graph. Can I calculate the avg of this slope function, by just looking a the 2 endpoints?  Surprisingly, you can now. Why does this happen. Because, with slope, if the slope goes up a certain magnitude above the avg, the slope has to come down the same magnitude below the avg, to give us the avg. It also follows from Mean Value Thm and from intuition. So, the jist is => The avg slope (rate of change of Y wrt X) of any function could be found by just looking at the 2 endpoints.
2. Area of a function: it can be calc as avg height of func multiplied by the width of the base. The avg slope of any func as seen above = [F(b)-F(a)]/(b-a), where a,b are endpoints on x axis. If we plot the slope function (i.e a function f(x) that is the slope of F(x) for all points on x axis), then the area of f(x) will be = Avg height of f(x) * base. But avg height of f(x) = avg slope of F(x) (as f(x) is slope func of F(x)). Since avg slope of F(x) =  [F(b)-F(a)]/(b-a),  that's the avg height of f(x). So, area of f(x) = avg height of f(x) * base =  [F(b)-F(a)]/(b-a) * (b-a) = [F(b)-F(a), which proves the theorem.

Diagram showing proof of Fundamenal Thm of Calculus

Finding area of a curve:

As we saw above, We use this formula for area under a curve from x axis (Y=0) to the function f(x): Area =   ^b
_a∫ f(x).dx  =   ^b
_a∫ y.dx (since f(x)=y). Other way to find area is to rotate the paper 90 degrees anticlockwise and then integrate with dy, i.e Area = ^f(b)
_f(a)∫ x.dy  Here limits a and b change to f(a) and f(b), since we are integrating along Y-axis. This gives the area of the remaining portion of the rectangle bounded by a, b, f(a), f(b). If we add up the 2 area, we should get the area of the rectangle minus the smaller rectangle = [b*f(b)) - a*f(a)].

ex: y=x^2. Area from x=1 to x=3 is  ^b=3
_a=1∫ y.dx = ^b=3
_a=1∫ x^2.dx = [x^3/3] from x=1 to x=3 => 1/3[3^3-1] = 26/3.

Now we take area along y axis. Then x=√y. Limits are y=3^2=9, 1^2=1. So, area from y=1 to y=9 is  ^b=9
_a=1∫ x.dy = ^b=9
_a=1∫ √y dy = 2/3* [y^3/2] from y=1 to y=9 => 2/3[9^3/2-1] = (26*2)/3.

The area of the rectangle formed is (3*9)-(1*1) = 27-1 = 26, which is the sum of 26/3+26*2/3=26. 

NOTE: Area of the figure under the X-axis is calculated as -ve while area above the x-axis is calc as +ve (automatically happens the way we integrate). If we want to find the absolute area, then we have to find the area of the regions separately and then add the absolute values of the 2 area.

Finding arc length of a curve:

To find the arc length, we use pythagoras thm in calculus.

Any length Δl² = Δx² + Δy² => Total length of arc from x=a to x=b is [∑Δl ] = [∑√ ( Δx² + Δy²) ] =  ∑[√ ( 1 + Δy²/Δx² )  * Δx] =  ^b
_a∫ √ ( 1 + dy²/dx² ) ] * dx  (by converting to integral) =   ^b
_a∫ √ ( 1 + f’(x)² ) dx  

2dl/dx = 2 + 2dy/dx (differentiating both sides wrt dx) => dl/dx = 1 + f’(x)

As we saw above, We use this formula for area under a curve from x axis (Y=0) to the function f(x): Area =   ^b
_a∫ f(x).dx  =   ^b
_a∫ y.dx (since f(x)=y). Other way to find area is to rotate the paper 90 degrees anticlockwise and then integrate with dy, i.e Area = ^f(b)
_f(a)∫ x.dy  Here limits a and b change

Finding Volume under a curve:

Generally for finding volume, surface area, etc, we need to use 2D calculus (involving both var dx and dy). But many times, these 3D figures are symmetric, and we are able to generate the 3D figures from the 2D figure by making concentric circles, etc. Then we can find volume or surace area by just using single variable, dx.

ex: Find volume of sphere: Here we take a circle at distance x from the center of sphere, and cut out this circle of thickness dx. Then all these slices of circles added up gives the volume of sphere. x^2+y^2=R^2. V = 2* ^b=R
_a=0∫ Π * y^2.dx = 2*Π* ^b=R
_a=0∫ [R^2-x^2]dx = 4/3*Π*R^3

Integral formulas:

Cheat sheet => https://tutorial.math.lamar.edu/pdf/Calculus_Cheat_Sheet_Integrals.pdf

As explained above, integrals are just inverse function of differentials. There are 2 types of integrals:

1. Definite integrals: When we provide limits on the integral (i.e finding integral for a function with limits of a->b.   ^b
   _a∫ f(x).dx ), then it's called a definite integral. The result will be a constant (with no "x" variable in it). This represents the area under the curve.
2. Indefinite integrals: When we don't provide limits (i.e ∫ f(x).dx), then  it's called an indefinite integral. The result will be a function of x, which is actually the inverse function (with a "x" variable in it). This represents the general solution, and so we need to add a constant C, i.e  ∫ f(x).dx) = F(x) + C. We add a constant C, as differential of constant gives 0, so any constant can be added to any function, and differential will still be the same.

Integration Rules:

• Constant Multiple Rule: ∫ k * f(x) dx = k * ∫ f(x) dx + C, where k is a constant. Constant C is added for all indefinite integrals, even if we don't write it everytime.
• Linear Transformation: If ∫ f(x) dx = F(x), then ∫ f(ax+b) dx = 1/a * F(ax+b). To prove, Choose u=ax+b => du=adx. Now substitute.
• Power rule: ∫ x^n dx = (x^(n+1))/ (n+1) + C (C is a constant).  It can be easily seen to be true as d/dx(x^n) = n*x^(n-1). Any func that can be broken down into polynomial with individual terms should use this formula to get integral
• Sum/Difference Rule: ∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx.
• Integration by Parts (or partial integration = PI): Written in 2 forms:
  • ∫ udv = u * v – ∫ v du, where u and v are differentiable functions. Can be proved from differentiation: d/dx(uv) = v.du/dx + u.dv/dx => d(uv) = vdu + udv => integrating both sides, we get ∫d(uv) = ∫udv + ∫vdu => uv =  ∫udv + ∫vdu => ∫udv = uv-∫vdu. For definite integral, this formula becomes  ^b
    _a∫ udv = uv| ^b
    _a -  ^b
    _a∫ vdu. If we write u=f(x) and v=g(x), then above form can be rewritten in terms of x as => ∫f.g´dx = f.g – ∫g.f´dx (exactly same form, just written differently)
  • ∫ [f(x).g(x)]dx = f(x)∫g(x)dx – ∫f'(x){∫g(x)dx}dx where f(x), g(x) are any two functions. This can be directly seen by choosing u=f(x) and v=∫g(x)dx (i.e dv/dx=g(x) => dv=g(x)dx). Now substituting u,v in formula above, we get ∫ udv = u * v – ∫ v du =>  ∫ [f(x).g(x)]dx =  f(x)∫g(x)dx –  ∫ { [ ∫g(x)dx] f´(x)} dx , which is the same form as what we wanted to prove. NOTE: We have f'(x) (derivative of f(x)) in last term and NOT f(x)).
  • This is a very imp formula used to solve integrals that can't be solved by any other method. There are rules on how to choose u and dv (i.e f(x) and g(x)). g(x) should be chosen such that you can integrate it easily. Remaining function is f(x), and derivative of this func f(x), which is f'(x) multiplied with G(x) (integrated function of g(x)) should also be integrable. This is tough to see for any arbitrary function. There's no hard rule on how to attack a function for PI, though some heuristics exist (shown below).
    
    • Wiki link => https://en.wikipedia.org/wiki/Integration_by_parts
    • ILATE heuristic rule => https://www.geeksforgeeks.org/maths/integration-by-parts/
    • Few ex explained very nicely => https://tutorial.math.lamar.edu/classes/calcII/IntegrationByParts.aspx
  • ex: ∫ ln(x)dx = xln(x) -x => this can only be solved by PI. Choose u=ln(x), dv=dx. This will allow us to solve, as both u, v are easily solvable.
• Partial Fraction decomposition (PFD): This is an useful technique to integrate polynomials of form P(x)/Q(x), where degree of Px(x) < degree of Q(x). We factor the denominator completely, and find corresponding terms for numerator.
  •  ex: ∫ 1/(x^2 + 5x + 6) = ∫ 1/[(x+3)(x+2)] = ∫ [1/(x+2) - 1/(x+3)] = ln(|x+2| - ln(|x+3|)
  • see more ex in cheat sheet above.

Some common integrals: (NOTE: integrals are just inverse function of differentials)

• ∫ e^x dx = e^x +C (C is a constant). It can be easily seen to be true as d/dx(e^x) = e^x.
• ∫ a^x dx = 1/ ln(a) * a^x as d/dx (a^x) = ln(a). a^x.
• ∫ 1/x dx = ln(|x|) as d/dx(ln x) = 1/x. We need to have absolute value of ln(x) as log is not defined for -ve number. If we have ∫1/(x.ln(a)), then 1/ln(a) being a constant, just gets taken out, and then ln(x)/ln(a) can be rewritten as log_a(x)
• Trignometric functions: Here we integrate trignometric func themselves, as well use trignometric substitutions to solve other regular integrals, which are otherwise impossible to solve.
  • First, recall few imp trig formulas:
    • sin²(x) + cos²(x) = 1. This is used to solve integrals of form √(1-x²). We substitute x with Cos(θ) or Sin(θ), doesn't matter.
    • sec²(x) = 1 + tan²(x). This is used to solve integrals of form √(1+x²) or  √(x²-1).  We substitute x with tan(θ) for  √(1+x²) and with Sec(θ) for √(x²-1).
    • csc²(x) = 1 + cot²(x).This is counterpart of above.
    • cos²(x) =1/2 [1 + cos(2x)], sin²(x) =1/2 [1 - cos(2x)]. Known as half angle/double angle formula. These 2 formulas are used to convert square of sin or cos into power of 1, which can easily be integrated. Without this formula, we won't be able to integrate sin²(x) or cos²(x). With this formula, it's 1 line integral.
  • Integrals of all 6 basic func of trig:
    • sin, cos => derived from differentiation itself.
      • ∫ sin(x) dx = -cos(x), 
      • ∫ cos(x) dx = sin(x),
    • tan, cot => take u substitution as u=sin(x) or u=cos(x). Similar for both tan and cot, ad pretty easy.
      • ∫ tan(x) dx= ∫ sin(x)/cos(x) dx. choose u=cos(x) => du = -sin(x) dx =>  ∫ tan(x) dx =  - ∫ (1/u)du =  -ln|u| = -ln|cos(x)| = ln|sec(u)|
      • ∫ cot(x) dx= ∫ cos(x)/sin(x) dx. choose u=sin(x) => du = cos(x) dx =>  ∫ cot(x) dx =  ∫ (1/u)du =  ln|u| = ln|sin(x)| (NOTE: no -ve sign with "ln")
    • sec, csc (cosec) => These are more intricate, as they involve PI and result in "ln" func.
      • for sec(x): ∫ sec(x) dx = ln |sec(x) + tan(x)|. Proof: ∫ 1/cos(x) dx = ∫ cos(x)/cos²(x) dx =  ∫ cos(x)/(1-sin²(x) dx. Take u=sin(x) => du=cos(x)dx => ∫ 1/(1-u^2) du =  1/2 * [ ∫ 1/(1-u) du + ∫ 1/(1+u) du ] = -ln(1-u) + ln(1+u) = ln[(1+u)/(1-u)] = 1/2* ln [1+sin(x) / (1-sin(x)]. No abs value is needed for term inside ln in this form, as (1+sin(x)) / (1-sin(x)) is always +ve. However if we write (1+sin(x)) / (1-sin(x)) as (1+sin(x))^2 / cos²(x) => 1/2* ln [1+sin(x) / (1-sin(x)].= ln [(1+sin(x) / cos(x)] = ln |sec(x) + tan(x)|. In this form, we have to take abs value.
      • For csc(x): same way as above. It's now   ∫ sin(x)/(1-cos²(x) dx. Integral is -ln |csc(x) + cot(x)|. Note the -ve sign in frnt of lln and also how inside the ln term, sec->csc and tan->cot.
  • Integrals that will yield the 6 basic func of trig (i.e the resul is the basic trig func). From derivatives of basic trig func, we also know the integrals that will yield the trig func
    • sin, cos: Remains same as above. 
    • tan, cot: ∫ sec²(x) = tan(x).  ∫ csc²(x) = -cot(x).  NOTE: there's -ve sign for  integral of csc²(x).
    • sec, csc: ∫ sec(x).tan(x) = sec(x).  ∫ csc(x).cot(x) = -csc(x).  NOTE: there's -ve sign for csc(x)
  • Integrals from derivatives of inverse or arc func:
    • ∫ 1/( √(1-x²) = sin^-1(x) or with -ve sign, it's cos^-1(x)
    • ∫ 1/(1+x²) = tan^-1(x) or with -ve sign, it's cot^-1(x)
    • ∫ 1/[|x|.√(x²-1)] = sec^-1(x) or with -ve sign, it's csc^-1(x)
  • Ex: When Integrals of form ∫ sinⁿ(x) * cos^m(x) or  ∫ tanⁿ(x) * sec^m(x) need to be solved, above trig formula come in handy.
    •  ∫ sinⁿ(x) * cos^m(x) => n.m can be odd or even (including n or m=0). n/m may be -ve intgers too. Below rules still apply.
      
      • ∫ sinⁿ(x) * cos^m(x): Here if one of them is odd, i.e m,n=odd (the other one may be even or odd or 0, doesn't matter), then take the one of those odd ones (let's say we have sin⁷(x)), then strip sin(x) and club it with dx (i.e sin(x)dx). Now, choose u=cos(x) and convert sin⁶(x) in form of cos(x). du= -sin(x)dx. So, now whole func is a poly in u, which can easily be integrated.
        • ex: ∫ sin⁵(x) * cos⁴(x) dx =  ∫ sin⁴(x) * cos⁴(x) sin(x)dx = ∫ (1-cos²(x))^2 * cos⁴(x) sin(x)dx = ∫ (1-u²)^2 * u⁴ du (by choosing u=cos(x), du = -sin(x)dx). Now integrate it as it's just poly.
      • ∫ sinⁿ(x) * cos^m(x): Here if both of them are even (n.m may be 0 too), then we first convert both func into same form (i.e either both sin or both cos). Now, we convert the obtained function into doubl angle formula (i.e convert into cos(2x)), and keep on doing it recursively, until we come down to power of 1 for sin or cos (whichever func we chose). 
        • ex: If it's just sin²(x) or cos²(x), then we can solve using formula 1/2 [1 +/- cos(2x)]
        • ex: ∫ sin⁶(x) * cos²(x) dx = ∫ (1/2 [1 - cos(2x)]) ^ 3 * (1/2 [1 + cos(2x)]) dx => Keep on expanding and multiplying, until you get to power 1.
    •  ∫ tanⁿ(x) * sec^m(x) => n.m can be odd or even (including n or m=0). n/m may be -ve intgers too. Here rules are slightly different than sin,cos case av=bove, as differentials are different here.
      • ∫ tanⁿ(x) * sec^m(x): Here if n=odd (m may be even, odd or 0, doesn't matter), then strip one tan and 1 sec into dx, substitute u=sec(x), convert tan(x) into sec(x) using trig formula.
        • ex:  ∫ tan⁵(x) * sec⁴(x) dx =  ∫ tan⁴(x) * sec³(x) tan(x).sec(x)dx = ∫ (u²-1)^2 * u³ du (by choosing u=sec(x), du = tan(x).sec(x).dx). Now integrate it as it's just poly.
      • ∫ tanⁿ(x) * sec^m(x): Here if n=even, then we have 2 cases:
        • m=even (including 0): This is a simpler case. Here we strip sec²(x), and remaining sec(x), we convert it into tan(x) [since it's even power, we can write it as tan²(x)]. Now substitue u=tan(x) => du=sec²(x)dx. Thus it becomes a poly, which can be solved easily. 
          • ex:   ∫ tan⁶(x) * sec⁴(x) dx =  ∫ tan⁶(x) * sec²(x) * sec²(x)dx =   ∫ tan⁶(x) * (1+tan²(x)) * sec²(x)dx = ∫ u^6*(1+u²)du (by choosing u=tan(x), du = sec²(x).dx). Now integrate it as it's just poly.
        • m=odd: This is harder case, as a lonely sec(x) with odd power will always remain. We convert tan(x) into sec(x) and exapnd. We'll end up with odd powers of sec(x). Intergal of sec(x) is known. Integral of sec³(x) is determined by Integral by parts (Link => https://www.analyzemath.com/calculus/Integrals/integral-of-sec%5E3(x).html). For even higher odd powers of sec(x), we recursively use integral by parts, until we get the final answer. (for sec⁵(x), Link => https://www.sarthaks.com/529606/evaluate-sec-5-x-dx)
          • ex: ∫ tan⁴(x) sec³(x) dx = ∫ (sec²(x) -1)^2*sec³(x) dx = ∫ [sec⁷(x) - 2*sec⁵(x) + sec³(x)]dx = Now integrate each term using Integration by parts (links shown above)
  • Trig Substitution: When integrals contain particular sq root forms, then substituing with trig func, and then converting back yields integral much more easily, than any other known method.

Details

Published: Wednesday, 23 April 2025 14:08

Hits: 1153

Telecom Companies:

Let's analyze Telecom Cos for investment purposes. These Co provide internet, mobile, TV or other services that basically relates to transfer of information by wire/wireless means.

Wiki => https://en.wikipedia.org/wiki/List_of_telecommunications_companies

Major source of revenue for biggest Telecom Co is mobile services (i.e your cell phone service), followed by internet services (known as Fixed line service) and TV (media) services.

Under Phone section, you can find more details on largest US Mobile operators and MVNO. Mobile operators in US: https://en.wikipedia.org/wiki/List_of_mobile_network_operators_in_the_United_States

Just Top 10 companies generate revenue of $1T. Probably all Telecom Co combined generate revenue of $2T or more worldwide (Just top 100 generate $1.5T, so remaining small players worldwide probably generate $0.5T, just a guess). Telecom Co routinely buy other Co (even unrelated to their main line of business) and routinely sell some of their assets (and buying them back again at higher prices) which make going thru there income statements and balance sheet very cumbersome. They also carry a lot of debt, and routinely issue new debt to buy other companies. They also pay a hefty dividend to shareholders, which is very common with public companies carrying an enormous amount of debt.

Even though net income is low at 10% of revenue, a big chunk of expense is in depreciation and amortization. If we take that out, these Cos generate lot more cash than income. However, their capital expenditure is also very high at >10% of revenue. 

FY 2024 Metrics:

Top 5 companies by revenue are:

1. China Mobile: It's Chinese state owned telecom Co. It's the largest mobile n/w operator in the world by subscribers and revenue. It used to be listed on NYSE, but was delisted in 2021 due to it's connection to Chinese People's Liberation Army. It was subsequently listed on SSE in China.
   
   • It had ~1B subscribers as of 2022. It's revenue has grown from $3B in 1997 to $150B in 2023 (mostly in a straight line), while it's earnings have grown from $1B to $25B. It's charging $150/yr per customer, which seems reasonable. It's market cap has been around $200B for the last 15 years (2010 - 2025), which is surprising as it's revenue/profits increased a lot, but didn't help the market cap.
2. Verizon: It's US  Company, which resulted from breakup of "Bell systems" (later renamed as AT&T) in 1983 into 7 regional Co. It was originally named "Bell Atlantic", but in 2000, changed the name to Verizon Communications after merging with telephone Co GTE in $65B deal. Verizon formed Verizon wireless in 2000 in a joint venture with Vodafone in a deal valued at $70B. It integrated it's own wireless divisions under "Verizon Wireless" and was planning an IPO for it in 2003, but later canceled it, as it made enough profits and didn't need any investor money. At that time, Verizon became the largest local telephone company in USA, operating 63 million telephone lines and 25 million mobile phone customers. In 2004, Verizon was added to DJIA index by kicking out AT&T. Verizon had expanded into optic fiber internet lines, but started divesting from this in 2005 to focus on wireless and Media. In 2006, Verizon bought MCI, a long distance provider for Business clients, for $8B, which caused it's revenue to inc by 20% in 2006. In 2008, Verizon acquired Rural Cellular Corp. for $2.7 billion, and wireless carrier Alltel for $28B. In 2010-2020, Verizon acquired more companies for bilions of dollars (2011=Terremark for $1.4B, 2012=AWS for $3.9B, 2015/2017=AOL and Yahoo for $5B each, and later sold them as part of it's media group for $5B to Apollo in 2021, 2016=>Fleetmetics for $2.4B along with some other companies, 2018=>XO communications for $1.8B, 2020=>Tracfone wireless for $6.5B, ). In 2013, it also bought remaining 45% stake in Verizon wireless from Vodafone for $135B (paid for by issuing 1.27B Verizon shares to Vodafone shareholders). As of 2024, Verizon is planning to buy fiber optic Co, Frontier Communications for $20B. All in all, Verizon has spent > $200B buying Companies in last 20 yrs mostly funded by issuing stocks
   • 146M wireless subscribers and 12M internet subscribers (7M Fiber Optic and 5M Fixed Wireless Access subscribers). It had $130B in revenue and a market cap of $200B.
3. AT&T: SBC  (one of the baby bells) acquired parent company AT&T Corp in 2005, and renamed merged Co as AT&T Inc., and retained it's logo and marketing. 4 of the baby bells along with parent AT&T are part of AT&T Inc. Other 2 baby bells merged to form Verizon. Cingular wireless (which had acquired old AT&T wireless in 2004) became AT&T subsidiary after SBC bought AT&T in 2006. AT&T acquired Time Warner Cable in 2016 for $110B, but later in 2022 divested completely of it's media arm as Warner Brothers Discovery which was listed as public company.  AT&T went from a revenue of $45B and profit of $7B in 2001 to $118B in revenue and $15B in profit in 2024.Their revenue went as high as $180B when they bought Time Warner, but declined later when they kept on selling their assets. They have mostly US customers, with o< 5% of revenue from Latin America. 2 Primary segments
   1. AT&T Wireless: 118M wireless subscribers. $85B in revenue in 2024, with operating income of $26B, so highly profitable segment. Only $65B came from services, remaining $20B was from equipment (i.e phone) sale. So, on an avg $600/yr per subscriber in phone services, which is very high compared to MVNO.
   2. Wireline (Fiber internet): $32B ($19B = business and $13B = consumer) in revenue in 2024. They made just $0.8B in operating income, though they used to make lot more (i.e in 2022 they made ~$3B in operating income on revenue of $34B). AT&T is getting rid of traditional copper based wireline. Out of total 14M connections in wireline, only 4M customers were on copper lines.
4. TMobile US: 130M wireless subscribers.
5. Comcast: 

Verizon (VZ):

Let's look closely at Verizon's financials from 2000 to 2025.

SEC filings => https://www.verizon.com/about/investors/sec-filings

Stocks outstanding: In 2000, there were 2.7B stocks, went to 2.86B in 2014. From 2004-2005, VZ spent $0.5B in buybacks, then in 2006-2008, it spent $6B. But stock count didn't go down at all due to dilution. Then in 2014, it increased share count by 1.3B shares (due to purchase of Verizon wireless) to 4.16B. To reduce stock count, in 2015, VZ again spent $5B, which brought stock count to 4.08B (it bought 80M shares for $5B). In 2021, VZ bought Tracfone by paying $3B in cash and $3B via 60M of VZ stock. Stock count rose by 120M during 2021 and 2022 getting to 4.2B. From 2023 onwards, stock count has been flat at 4.21B on Jan 31, 2025, which is a good sign.

2 units in business:

1. Consumer reporting unit (CU)
2. Business reporting unit (BU)

Debt:

Assets:

• Wireless License: Carrying value = $156B. It's substantially iess than the fair value estimated based on cash flow. Basically meaning that VZ should be able to resell these licenses for much more than $156B
• Goodwill => The balance = $23 billion, of which ~$21 billion was in our Consumer reporting unit and ~$1.7 billion was in our Business reporting unit. At end of 2023, goodwill in CU was $7.5B, but a impairment of $5.8B reduced it to $1.7B. Gooodwill in CU was way above fair value.

Details

Published: Monday, 31 March 2025 04:14

Hits: 612

Central AC - DIY

Installing a Central AC:

This is NOT a DIY. It's always installed by a professional. There are videos on how to do it yourself, but you would be better installing a ductless minisplit (may be multiple of them) to achieve the same result. Minisplits are DIY and lot easy to replace.

Replacement of AC: AC replacement labor is pretty expensive at $4K per installation just in labor cost. It's definitely a DIY, but only for people who have already handled minisplit Installation and repair. Here's 2 part video explaining it:

Part 1 (Replacing outside condensor unit): https://www.youtube.com/watch?v=sR5wIbNrs7Y

Part 2 (Replacing inside Evaporator coil): https://www.youtube.com/watch?v=oIDSNBOpBKg

Part 3 (Brazing and Pressure test): https://www.youtube.com/watch?v=mUwIKPoBYSo

Repair and Maintenance:

TUNEUP:

A lot of companies want to do "tuneup" for your AC and heating system for $100's of dollars. Most of the time, they are not really finding or fixing issues, but actually trying to upsell on problems that don't exist. Home Depot and Lowes offer "AC tuneup" specials for low price of $10-$30 per AC unit. I've used them at $30/unit (total $60 for 2 AC units) and felt it was a total wastage of money. They measure AC freon pressure, check capacitor values, drain water thru the pipe and then try to upsell. You can check all these things yourself. Home Depot and Lowes, both use, ARS Resue Rooter as their HVAC contractor in my area. Their technicians didn't seem interested at all in tuning up anything, or even sharing the details of what they measured (stating that I won't understand these). I never got the report, even though I called them and asked them to send me the report.

AC tuneup deals:

• 11/27/2025: AC tuneup for $9 at HomeDepot. At this price, it's worth it, even if they do nothing.
  • Link => https://slickdeals.net/f/18884137-hvac-heating-or-ac-tuneup-8-88-at-home-depot?src=frontpage

DIY REPAIRS:

A lot of common problems with AC are easy to fix, and you don't have to sell your kidneys to pay someone to repair it.

Video showing top 4-5 issues with AC issues and repairs (Taddy digest) => https://www.youtube.com/watch?v=wThzFULXxN8

1. Freon Topoff: 

Most of the repair of Central AC is around Freon leaking, which is a very common issue. Some Freon leaking is OK, as you can just top off every couple of years, instead of trying to find the leak and fixing it. However, AC repair companies which come and top off Freon charge a lot of money, usually around $100/lb, while you can get freon for around $10-$20 per pound.

Here's a video detailing how to do it => https://www.youtube.com/watch?v=J1s4wxDBe24

One more excellent 30 min vid from AC Service Tech => https://www.youtube.com/watch?v=qpXZhTRPIXc

Look for High side and low side pressures to be inline with what it's supposed to be. For R10A, you want low side pressure to be around 120PSIG, while high side pressure to be around 400 PSIG. It depends a lot on ambient temps (both indoor and outdoor) though.

Freon leak detection: This is harder and requires more tools. I've explained it under "Minisplit" section. Look for leak detection by first topping off freon, and checking with "Refrigerant leak sensor". On top of that, you can put soapy water at places you suspect of leak. If the AC is showing < 50 PSI (meaning most of the refrigerant has leaked), then you can vacuum out the AC, and then add nitrogen gas to it and do leak detection again. This process is more involved for AC than Minisplit.

2. Capacitor Replacement:

A lot of time, your AC will just die (not start at all) on a hot summer day. The most common culprit is the Capacitor that's on the outside unit. It's a dual capacitor (2 capacitors in 1 pkg), and is just connected via wires. The capacitor is usually inside the covering to protect electrical connections, so you have to unscrew the little covering on the side of the unit to see the capacitor. You can measure the cap b/w the 3 terminals via multimeter. The multimeter should show open (or infinite resistance) is the capacitor is good. If it shows close to 0 resistance, that means there' s a short in the capacitor, and the capacitor needs to be replaced. Sometimes the capacitor is not out right shorted, but has a lower capacitance value than what it's supposed to have. That means it''s out of spec and will fail in some time. This can't be detected by a multimeter, but you can buy the more advanced meters which measure capacitance too. This will give you the proper capacitance reading. It's better to replace them if they are out of spec, instead of waiting for them to fail. You can buy these capacitors from Home Depot, Lowes, etc for $10 a piece. The only spec that needs to match is capacitance value listed. It's written in MFD (micro farad) or uF. There are 2 cap values mentioned, ad you need to match with the new one that you are going to replace with. You do NOT need to match the part name from the printing on the capacitor. If you can't read the Cap value, then you need to call the manufacturer of your AC and they'll give you the part number and the cap values. Ignore the part number, as you can buy any brand of cap from anywhere. If a HVAC contractor comes to fix this, he'll charge you $300-500 for replacing these capacitors. It's a 2 minute job and saves you $$$.

Capacitor replacement (DIY HVAC guy) => https://www.youtube.com/watch?v=FQisFmMtAis

The 3 terminals of Cap are: C (common), FAN (fan) and HERM(Hermetic compressor). So, the 2 cap formed are b/w C-FAN, and b/w C-HERM. If you measure cap values b/w these you will see the values. HERM cap (~50uF) is listed 1st on the pkg, and it's always lot higher than the FAN cap (~5uF) which is listed next (i.e HERM_CAP/FAN_CAP). These are the 2 motors in the outside unit => one that cools the condensor (the visible big fan that you see, which is not a very powerful motor) and the other is the compressor motor that does the job of compressing to increase the pressure of refrigerant. This motor has to be lot more powerful to be able to do the pressurizing job efficiently, hence the higher cap.

The colored wires that connect to Caps in my AC are: Red is common, Purple is Fan and Yellow is Herm. It may be same or different colors. Make a note of these colors and what they connect to, so that you connect them exactly as it was before.

Link with details => https://hvactrainingshop.com/dual-run-capacitor/

My 3.5 TON AC from Lennox (for downstairs) read 44.74uF(HERM), 10.06uF(FAN), while specs were 45uF(HERM), 10uF(FAN). So, both the caps were good as they were within 1% of Spec. Even then, I bough one to keep for spare from here (I just looked for MFD 45uF + 10uF MFD, it came with 5 yr warranty, and is less than 1/2 the price of one from Lennox) => https://www.amazon.com/gp/product/B0932QKL5L

Similarly for 2 Ton AC from Lennox (for upstairs) read 34.5uF(HERM), 4.44uF(FAN), while specs were 35uF(HERM), 5uF(FAN). So, Fan Cap was bad as it was outside 10% spec. Even though the AC is running fine, it's not advisa;e to run AC with Caps which are more than 10% outside of spec. So,, I bought one from same company => https://www.amazon.com/gp/product/B0932RGKCX

Each of them cost $15 for a total of $30. HVAC Tune up guy gave me a quote of $700 for replacing both. Now that's a ripoff :(